No.1143 最长公共子序列

给定两个字符串 text1 和 text2，返回这两个字符串的最长 公共子序列 的长度。如果不存在 公共子序列 ，返回 0 。

一个字符串的 子序列 是指这样一个新的字符串：它是由原字符串在不改变字符的相对顺序的情况下删除某些字符（也可以不删除任何字符）后组成的新字符串。

例如，"ace" 是 "abcde" 的子序列，但 "aec" 不是 "abcde" 的子序列。 两个字符串的 公共子序列 是这两个字符串所共同拥有的子序列。

示例 1：

输入：text1 = "abcde", text2 = "ace"
输出：3
解释：最长公共子序列是 "ace" ，它的长度为 3 。

示例 2：

输入：text1 = "abc", text2 = "abc"
输出：3
解释：最长公共子序列是 "abc" ，它的长度为 3 。

示例 3：

输入：text1 = "abc", text2 = "def"
输出：0
解释：两个字符串没有公共子序列，返回 0 。

提示：

• 1 <= text1.length, text2.length <= 1000
• text1 和 text2 仅由小写英文字符组成。

解题思路

最长公共子序列问题是典型的二维动态规划问题。

状态

假设字符串 text1 和 text2 的长度分别为 m 和 n，创建 m+1 行 n+1 列的二维数组 dp，其中 dp[i][j] 表示 text1[0:i] 和 text2[0:j] 的最长公共子序列的长度

上述表示中，text1[0:i] 表示 text1 的长度为 i 的前缀，text2[0:j] 表示 text2 的长度为 j 的前缀

边界

1. 当 i = 0 时，text1[0:i] 为空，空字符串和任何字符串的最长公共子序列的长度都是 0，因此对于任意 0<=j<=n，都有 dp[0][j] = 0；

2. 当 j = 0 时，text2[0:j] 为空，空字符串和任何字符串的最长公共子序列的长度都是 0，因此对于任意 0<=i<=m，都有 dp[i][0] = 0；

3. 因此：当 i = 0 或 j = 0 时，dp[i][j] = 0；

4. 当 i > 0 且 j > 0 时，考虑 dp[i][j] 的计算：

   • 当 text1[i-1] = text2[j-1] 时，将这两个相同的字符称为公共字符。考虑 text1[0:i-1] 和 text2[0:j-1] 的最长公共子序列，再增加一个字符（即公共字符）即可得到 text1[0:i] 和 text2[0:j] 的最长公共子序列。因此：dp[i][j] = dp[i-1][j-1] + 1；
   • 当 text1[i-1] != text2[j-1] 时，需要考虑 text1[0:i-1] 和 text2[0:j] 的最长公共子序列；以及 text1[0:i] 和 text2[0:j-1] 的最长公共子序列。要得到 text1[0:i] 和 text2[0:j] 的最长公共子序列，应取两项中长度较大的一项，因此： dp[i][j] = max(dp[i-1][j], dp[i][j-1])。

状态转移方程

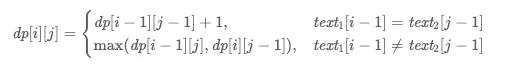
最终得到 dp[m][n] 即为 text1 和 text2 的最长公共子序列的长度。

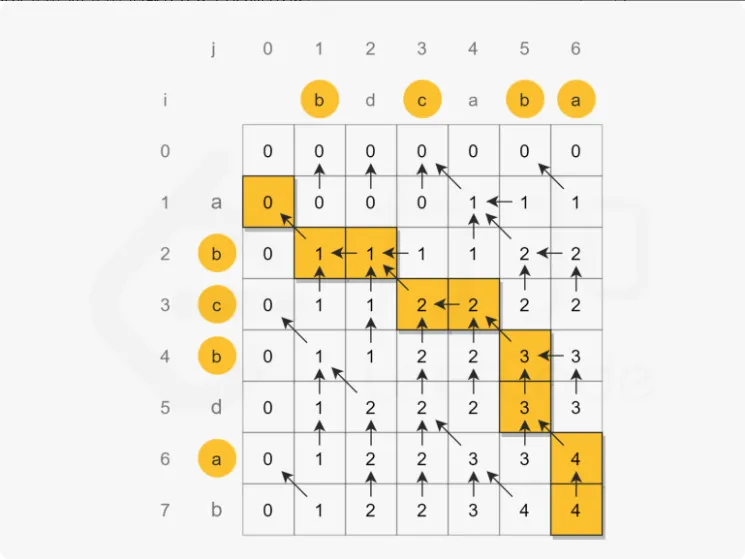
实现

动态规划

/**
 * 二维动态规划
 * @param {string} text1
 * @param {string} text2
 * @return {number}
 */
var longestCommonSubsequence = function (text1, text2) {
  let m = text1.length;
  let n = text2.length;
  let dp = new Array(m + 1).fill(0).map(() => new Array(n + 1).fill(0));
  for (let i = 1; i <= m; i++) {
    const str1 = text1[i - 1];
    for (let j = 1; j <= n; j++) {
      const str2 = text2[j - 1];
      if (str1 === str2) {
        dp[i][j] = dp[i - 1][j - 1] + 1;
      } else {
        dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
      }
    }
  }
  return dp[m][n];
};